第六讲:色彩和色彩空间·下篇
在前两篇推文中,我们了解了色彩空间、像素、图像和视频之间的组成关系,并且比较详细的学习了色彩空间 RGB、YUV 的采样&存储格式。今天,我们基于这些内容,再补充一些重要的关联知识。
我们已经知道,像素是图像的基本组成单元,所以对视频图像的存储,实际上是对像素的存储。计算机在处理图像时,需要按一定规则将像素数据从内存中读取出来。这里的“规则”,首先基于色彩的采样 & 存储格式,其规定了色彩分量的“存储顺序”以及“分平面存储逻辑”。但仅知道这些信息,对“单纯”的计算机来说还是不够的,我们必须明确地告诉它:要读取多少字节长度的数据,这里就会引申出 “定量” 的规则。
图像位深
由点及面,先从像素开始,了解每个像素在计算机里是如何“定量”存储的,再扩展到视频图像上。要学习这部分内容,先给大家介绍一个新面孔:图像位深。
其实,在之前 音频要素 的推文中,我们已接触到 “音频采样位深” 的概念。音频采样位深,指的是用多大的字节空间来存储声音的量化值。一般来说,音频采样位深越大,则声音采样量化的精度越高、失真越少。现在,我们要把位深的概念延伸到视频图像领域。
在视频图像领域,关于位深的概念比较多,诸如:通道位深、像素位深、色彩位深和图像位深等。为了避免混淆,在本文中我们要将相关定义统一一下,并以 RGB 图像举例说明如下。
对于 RGB 图像,如果我们分别使用 8bit (1个字节)来存储色彩空间的各个通道分量,则一个完整的 RGB 像素将占用 3*8 = 24bit 空间(3个字节)。此时,我们称:
-
通道位深:8bit,表示存储色彩空间的一个分量(通道)需要 8bit 空间;
-
像素位深:24bit,表示存储一个 RGB 像素需要 24bit 空间。
注:本文中,除非特别说明外,我们提及的图像位深均指像素位深。
需要补充的是,图像位深 24bit 、通道位深 8bit 是比较标准的位深配置,大家可能还会接触到诸如 32bit、16bit、8bit 等图像位深,它们并不是 3 的倍数,无法平摊到 RGB 或者 YUV 的三个通道上。我们应该如何理解这些 “不规则” 的图像位深呢?
其实,我们只要确认到具体的通道位深,就可以比较清晰的理解了,如下:
-
32bit 图像位深:在 24bit RGB 图像的基础上,增加了一个 8bit 的透明通道 A。比如我们上篇推文提到的 RGBA、BGRA 等等,可以称为 RGBA32、BGRA32;
-
16bit 图像位深:R、G、B 通道分量,分别使用 5bit、6bit、5bit 通道位深 ,可以称为 RGB565;
-
8bit 图像位深:R、G、B 通道分量,分别使用 2bit、3bit、3bit 通道位深,可以称为 RGB233。
除上述举例外,还会有诸如 RGBA4444、RGB555 等等情况。当脱离本文范畴,大家在实际应用中接触到图像位深时,仍需要明确其具体含义,究竟是像素位深、还是通道位深、每个通道又是怎么分配的,避免混淆。
现在,让我们再回到图像位深为 24bit 、通道位深为 8bit 的配置上。在该配置下,RGB 的每一个通道分量可表示 2^8 = 256 个值。这意味着,如果仅考虑 R 分量,就会有 256 种深浅不同的红色。以此类推,三个通道综合,即可以得到 (2^8)^3 = 16,777,216 种不同的组合,每种组合表示不同的颜色。这也就是之前的推文中我们说 “RGB 色彩空间可以表示约 1677 万种色彩” 的原因。
显然,图像位深越大,其像素可表示的颜色数量就越多,视频图像的色彩自然也就越丰富、细腻,在色彩渐变处也会更加平滑。有一个比较极端的比喻可以用于帮助理解:试想我们要绘制一幅包含了七色彩虹的画,那么拥有七支不同颜色的画笔(高位深)和 只拥有单颜色的画笔(低位深),在绘制效果上自然会呈现出巨大的差异。
参考下图,分别为同一张图像,在 24bit 位深、8bit 位深(2^8 = 256 种颜色)、 4bit 位深(2^4 = 16种颜色)下的表现。
图1:24 bit
图2:8 bit
图3:4 bit
可以看到,在 24bit 图像位深下,蓝天、云彩、企鹅绒毛的颜色自然细腻、过渡平滑,画面主次鲜明。而位深越低,由于可表示的颜色数量减少,部分颜色数据丢失并被替代,开始出现颜色趋同或断层,画面也越发的不自然。除了降低位深外,位深 24bit 若往上升,也有更高的 30bit(通道位深 10bit )、36bit(通道位深 12bit )等等。
那么问题来了,参考上面的对比效果,我们是否应该无条件地使用高位深呢?
答案是否定的。
需要注意的是,虽然图像的位深越大,能够表示的颜色越多,但相应需要的存储空间也越大,传输所需的带宽也越多,带来成本的提升,对于软硬件的要求也更苛刻。更何况,24 bit 图像位深已包含 1677 万种颜色,这远远超过了人眼的视觉感知能力,足以满足绝大部分业务场景。综合考量,现阶段仍主要使用 24 bit 的图像位深。
以上就是本期课程关于图像位深的相关知识。
图像宽高(Width、Height)与跨距(Stride)
再回到全文的开始:“图像的基本组成单元为像素,对视频图像的存储,实际上是对像素的存储”。基于图像位深,我们可以确定存储一个像素所需的字节数,下面,可以开始“指导”计算机如何定量读取图像数据了。
像素在图像中是一行一行排列、并逐行存储在内存中的,计算机在读取图像时,就需要逐行地、正确地读取出每一行的像素。这里就引出两个问题:每一行究竟有多少个像素?计算机每获取一行数据需要读取多少个字节呢?要解答这两个问题,我们需要再学习两个概念:图像的宽高 (Width、Height) 和跨距 (Stride)。
1 图像宽、高
说到图像的宽高,大家直觉上可能会联想到 “厘米”、“英寸” 等长度单位,其实,从图像处理的角度并非如此。在视频图像处理上,描述图像宽高时,通常使用的是“计数单位”,而其具体的数值,则由图像的分辨率决定。
关于视频图像的分辨率,在系列推文中还没有和大家正式介绍,但大家对 “分辨率” 肯定是不陌生的。在各大视频/图片网站上、在各种视频/图像文件规格中,我们常看到诸如 540x960(540P)、720x1280(720P)、1080x1920(1080P)等参数,它们就是所谓的分辨率,其表示的含义为:图像在水平方向、垂直方向上,每行、每列的像素 “个数”。
-
宽(Width):水平方向每行的像素个数,等于图像分辨率的宽
-
高(Height):垂直方向每列的像素个数,等于图像分辨率的高
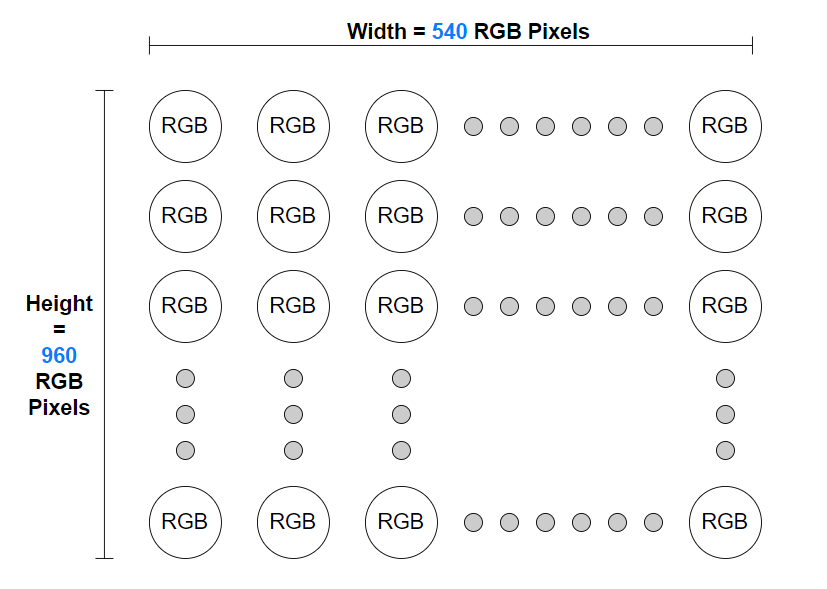
如下图所示,对于分辨率为 540x960 (宽 x 高)的 RGB 图像,其水平方向每行有 540 个 RGB 像素,垂直方向每列有 960 个 RGB 像素。
图4:像素排布,分辨率 540x960,宽 x 高
不难发现,分辨率宽高相乘得到的数值 = 图像中像素的总个数,540 x 960 的 RGB 图像中包含 518400 个像素,分辨率越高,像素的个数也就越多。
关于分辨率的知识,我们今后还会有专题作进一步讨论,今天大家了解到分辨率与图像宽高、像素个数的关系即可。
现在,我们已经通过分辨率信息,确定了图像每行的像素个数,可以尝试计算每行数据的长度(字节)。因为视频图像的处理通常是逐行进行的,计算机更关注每行有多少数据,而对于具体有多少行(Height)没有太多的要求。
以 24bit 的 RGB 图像为例,假设分辨率为 538 x 960,因为每个像素的 R、G、B 分量都连续存储在同一平面上(详见前文 色彩和色彩空间-中篇),我们可以通过如下步骤,计算每行像素的字节长度:
-
每行像素的个数 = 图像分辨率宽 = 538
-
每行像素的字节长度 = 像素位深 x 每行像素的个数 = 24 bit x 538 = 1614 byte( 注:1 byte = 8 bit)
如上,我们得到结论:对于分辨率为 538 x 960 的 RGB 图像,每行有 1614 byte 数据。计算过程看起来清晰明了,有理有据,于是我们信心满满地将 1614 byte 这个字节长度告知计算机,计算机也一丝不苟地按要求去读取一张 538x960 的图片。却可能会得到如下的结果:
图5:原图,分辨率 538x960
图6:按每行1614 byte数据,进行读取和渲染
我们发现,实际渲染出来的图像,呈现出规则的斜条纹,与原图相比已面目全非。
为什么会出现这样的问题呢?难道是计算机出现了 Bug ?或者说,计算机是无辜的,图像每行的像素个数实际上并不等于图像的分辨率宽度 ?要解答这些问题,我们就需要了解另外一个概念:跨距 (Stride)。
2 图像跨距
我们知道,计算机的处理器主要是 32 位或 64 位的,当处理器执行运算时,一次读取的完整数据量最好为 4 字节 或 8 字节的倍数。如果我们要求计算机读取非 4 字节或 非 8 字节对齐的数据,它就需要进行额外的处理工作。额外工作的引入,势必会影响效率和性能。为了规避这样的问题,就需要在原始数据的基础上,再增加一些“无效数据”,使待处理的数据量对齐到 4 字节 或 8 字节 。这样计算机才能以最高效的方式工作。当然,对齐规则也不一定是 4字节/8字节 的倍数,实际仍取决于具体的软硬件系统。
回过头来,看看前面计算得到的 “1614 byte”,大家是否发现问题了呢?
是的,这并非一个 4 字节或 8 字节倍数的数值。所以,基于前述的考量,如果在一个要求 4 字节 或 8 字节 对齐的系统内存中存储该图像,往往需要增加一些额外数据,将 1614 byte 对齐到比如 1616 byte。而这里的 1616 byte,即称为图像的跨距 (Stride)。
跨距 (Stride),是图像存储在内存中,每一行数据所占空间的真实大小,它大于或等于通过图像分辨率宽度计算的字节长度。每读取一个 Stride 长度的数据,意味着完整读取了图像的一行,下次读取就该“换行”了。其中,用于补齐至 Stride 而增加的额外数据,我们称之为填充(Padding)。Padding 仅影响图像在内存中的存储方式,无需(也不可以)用于实际渲染。
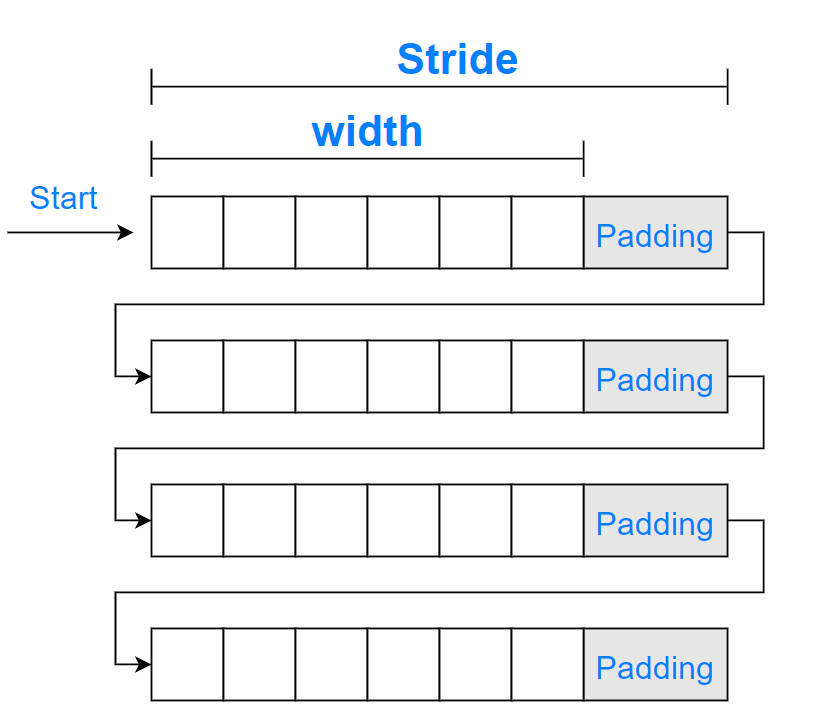
我们可以通过下图,直观的理解 Width 、Padding 和 Stride 的关系。
图7:Width 、Padding 和 Stride
参考上图,从 Start 位置开始, 计算机只有按 Stride 读取每一行图像数据,再按 Width 进行实际的渲染,避免将无效的 Padding 渲染出来,才能显示出正常的图像。如果仅使用 Width 计算 Stride(比如上面,我们告诉计算机将 Stride 设置为 1614 byte),那么就可能会误将部分 Padding,视为有效的图像数据进行渲染,行与行之间的像素相对位置也将发生累计偏移,出现诸如斜条纹等异常。
我们也可以通过一些简化的方式,来理解斜条纹产生的原理。
参考下图,我们先忽略“字节长度”,简单地把图像数据、填充数据的单位都统一至“像素”。假设原图的 Width x Height = 6 x 8,存储时将 Stride 对齐为 8。图中彩色部分为真实图像(原图左侧),黑色部分为填充的 Padding(原图右测),中间存在的空白间隙仅为方便区分。
图8:原图, Stride = 8,Width = 6
若使用正确的配置, Stride = 8 进行读取,Width = 6 进行渲染,则仅会显示出彩色部分, 黑色部分的 Padding 在渲染时会被忽略。
如果使用错误的 Stride = 7,正确的 Width = 6,会出现如下问题:从第一行开始,少读取了一块 Padding,并将这部分少读取的 Padding ,误当作第二行的 “有效图像” 进行读取、排列。最终,计算机再以 Width = 6 进行渲染时,将得到如下图像,出现了右侧下沉的斜条纹效果。
图9:错误,Stride = 7,Width = 6,右侧下沉的斜条纹
同理,Stride 偏大、Width 偏大、Width 偏小,都会影响图片的读取和渲染,大家在处理时需要注意。我们在下面也展示出相关的简化参考图:
图10:Stride = 9,Width = 6,左测下沉的斜条纹
图11:Stride = 8,Width = 7,多渲染出一列Padding数据
注意,实际应用中如果 Padding 数据被错误渲染出来,不一定都是黑色的,具体由填充的数据而定。如果都使用 0 值填充,那么 RGB 图像的 Padding 为黑色,YUV 图像的 Padding 则为绿色。其他可能的错误情况,大家可以自己尝试推演一下,在此就不过多展开。
3 分平面 YUV 的 Width、Stride
上面对于 Width 、Stride 的讨论,都是基于 RGB 图像来举例。对于 RGB 图像,其色彩空间分量是同一平面、连续存储的,一般只需考虑一个平面的 Width 和 Stride。
而 YUV 图像比较特殊,它可能使用分平面( Planar 、Semi-Planar )的存储方式(详见色彩和色彩空间-中篇)。
从整个图像的角度看,YUV 图像的每一行依旧有 Width = 720 个像素。但是从存储的角度看,Y、U、V 分量可能存放在不同的平面,计算机想要理解 YUV 色彩,就需要知道:在每个平面上、每次要读取多少数据,才能正确地组合成原始图像的一行像素。
“在每个平面上、每次要读取多少数据”,意味着需要知道每个平面的 Width 和 Stride。而考虑到 U、V 分量相对于 Y 分量可能有降采样,各个分量平面的 Width、Stride 可能不同, 必需要按存储规则分别求取。
下面,我们针对常见的 YUV 格式:I422、 I420 和 NV21 ,具体讨论一下,何谓分平面的 Width 和 Stride。
我们将基于通道位深 = 8 bit,图像分辨率 Width = 720,Height = 1280,展开后续内容的讲解。为方便理解、简化过程,我们假设处理器以 4 字节对齐,通过各平面 Width 计算得到的数据长度若满足 4 的倍数,即可作为各平面的 Stride,无需考虑 Padding 填充。
关于这三种 YUV 格式的采样&存储原理,大家可详细参考上一篇推文 色彩和色彩空间-中篇,下面用到时仅做简述。
由于 I422、 I420 和 NV21 的 Y 平面采样逻辑相同,Y分量均为全采样,我们先统一进行计算。
对于 Y 平面,因为 Y 分量为全采样,故:
-
Width_Y_Plane = 每行 Y 分量个数 = 图像每行像素个数 = Width = 720
-
Stride_Y_Plane = Width_Y_Plane x 通道位深 = Width_Y_Plane x 8 bit = 720 byte
注:因为 Width_Y_Plane x 8 bit = 720 byte 满足预设的对齐要求,故直接作为 Stride_Y_Plane,实际应用中,需要另外进行确认。后面若有类似处理,不再重复说明。
对于 U、V 平面, 因为 U、V 分量在不同 YUV 格式下有不同的采样、存储逻辑,需要按规则具体计算。
3.1 I422
I422 的采样和存储逻辑简述为:
-
采样:Y 分量全采集,宽度方向每两个 Y 分量共用一组 UV 分量,高度方向每行独立采集 UV 分量
-
存储:Y、U、V 分别存储于三个平面,对于一个宽度为 4 个像素、高度为 2 个像素的采样区域,三个平面分别为 4x2、2x2、2x2 的数组
对于 U 平面, U 分量水平方向的采样为 Y 分量的 1/2,故:
-
Width_U_Plane = 每行 U 分量个数 = 每行像素个数/2 = Width/2 = 360
-
Stride_U_Plane = Width_U_Plane x 通道位深 = 360 byte
对于 V 平面,其采样存储逻辑与 U 平面一致,故:
- Stride_V_Plane = Width_V_Plane x 通道位深 = 360 byte。
如果使用数组 Stride_I422[3] 记录三个平面的跨距(字节长度),即有 Stride_I422[3] = { Width, Width/2, Width/2}(使用 Width 的数值大小来表示)
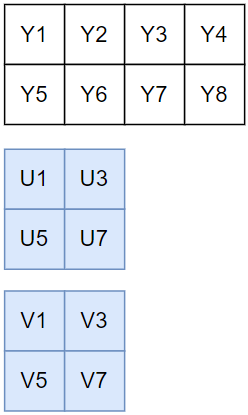
3.2 I420
I420 的采样和存储逻辑简述为:
-
采样:Y分量全采集,宽度方向和高度方向每四个 Y 分量共用一组 UV 分量,也即第二行复用第一行的 UV 采样;
-
存储:Y、U、V 分别存储于三个平面,对于一个宽度为 4 个像素、高度为 2 个像素的采样区域,三个平面分别为 4x2、2x1、2x1 的数组。
对于 U 平面,U 分量水平方向的采样为 Y 分量的 1/2(每行),故:
-
Width_U_Plane = 每行 U 分量个数 = 每行像素个数/2 = Width/2 = 360
-
Stride_U_Plane = Width_U_Plane x 通道位深 = 360byte
对于 V 平面,其采样存储逻辑与 U 平面一致,故:
- Stride_V_Plane = Width_V_Plane x 通道位深 = 360byte
如果使用数组 Stride_I420[3] 记录三个平面的跨距(字节长度),即为 Stride_I420[3] = { Width, Width/2, Width/2 }
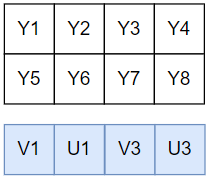
3.3 NV21
NV21 的采样和存储逻辑简述为:
-
采样:Y分量全采集,宽度方向和高度方向每四个 Y 分量共用一组UV分量,也即第二行复用第一行的 UV 采样
-
存储:Y、UV 分别存储于两个平面,对于一个宽度为 4 个像素、高度为 2 个像素的采样区域,两个平面分别为 4x2、4x1 的数组,UV 共同存储于第二个平面,并按 V、U 的顺序交错存放
对于 UV 平面,因为 U 、V 水平方向采样均为 Y 分量的1/2(每行) ,并且连续交错存储,故:
-
Width_UV_Plane = 每行 U分量个数 + V 分量个数 = 每行像素个数/2 + 每行像素个数/2 = Width = 720
-
Stride_UV_Plane = Width_UV_Plane x 通道位深 = 720 byte
如果使用数组 Stride_NV21[2] 记录两个平面的跨距(字节长度),即为 Stride_NV21[2] = { Width, Width }
需要特别注意的是,虽然综合所有平面来说,I422、I420、NV21 每次读取的 Stride 总和,均为 Width x 2 :
-
Stride_I422[0] + Stride_I422[1] + Stride_I422[2] = Width x 2
-
Stride_I420[0] + Stride_I420[1] + Stride_I420[2] = Width x 2
-
Stride_NV21[0] + Stride_NV21[1] = Width x 2
但对于 I420 和 NV21,因其 “宽度方向和高度方向每四个 Y 分量,共用一组UV分量” 的特性,每次读取 U、V 平面、或 UV 平面的一行数据,实际是供 Y 平面的两行数据共用的。因此,平均下来,读取整张图像的数据总量会存在差异:
-
Data_I422 = Data_Y + Data_U + Data_V
= Height x Width + Height x Width/2 + Height x Width/2
= Height x Width x 2
-
Data_I420 = Data_Y + Data_U + Data_V
= Height x Width + Height/2 x Width/2 + Height/2 x Width/2
= Height x Width x 1.5
-
Data_NV21 = Data_Y + Data_UV
= Height x Width + Height/2 x Width
= Height x Width x 1.5
可以看到,Data_I422 大于其余两个。这也证明了 ,YUV420 相对于 YUV422,前者采样数据量更小、压缩率更大。
总结
以上,即为常见 YUV 格式 Width 、 Stride 的计算方法。如果大家在理解上有些难度,可以再回顾一下 色彩和色彩空间-中篇 的内容,结合进行梳理。需要再次强调的是,为方便理解,上面的讲述中默认: 使用 Width 直接计算得到的 Stride 符合对齐要求,无需考虑 Padding 填充,而实践中考虑到不同系统、硬件芯片的对齐处理差异,真实的 Stride 是否要做补齐,仍需再具体确认。
至此,关于计算机如何正确地 、“定量” 读取视频图像数据,我们也有了一定的了解。考虑到硬件芯片、操作系统的多样性,色彩空间采样&存储格式的多样性,要完全厘清所有的 “定量” 规则,还是比较麻烦的。
不过,在使用 “自定义视频采集” 功能时,前面提及的色彩空间、采样&存储格式、Width 和 Stride 等概念,就需要你了然于胸,否则就可能出现诸如“斜条纹”的问题。
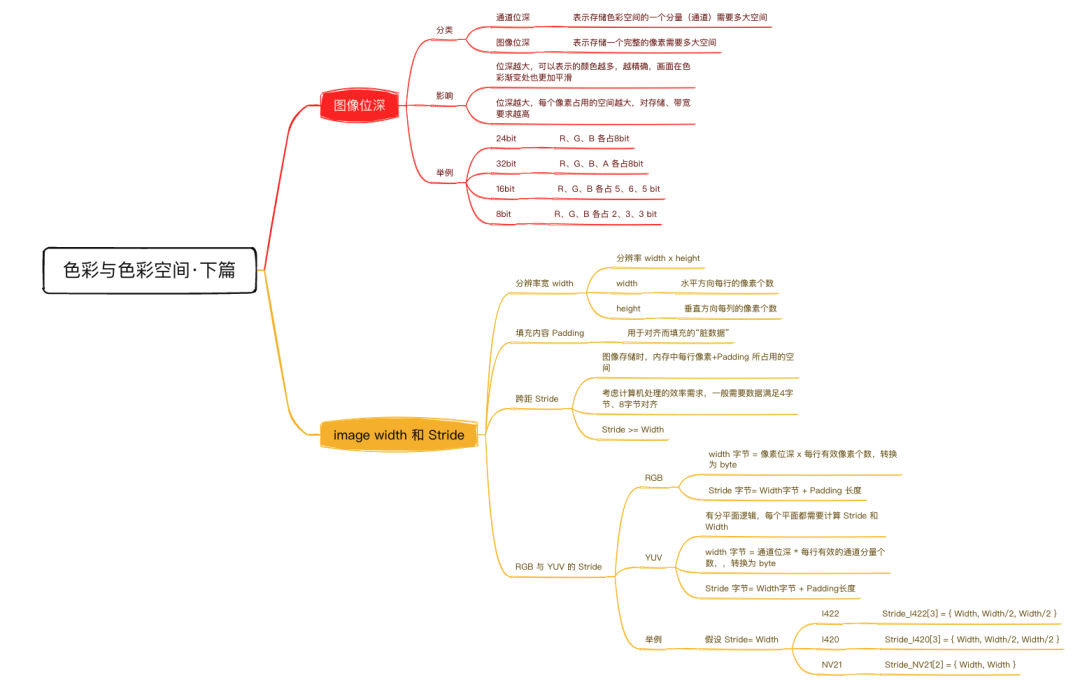
最后,我们通过一个思维导图,再梳理一下本文的核心内容。
参考推文中的举例,假设原图的 Width x Height = 6 x 8,存储时将 Stride 对齐为 8。当使用 Stride = 8,Width = 4,进行读取和渲染,会出现什么问题?
思考题
上期思考题揭秘
问
作为请参照 YUV 采样格式的“规则”,说明 YUV 4:1:1的采样逻辑。
答
对于一个宽度为 4 个像素、高度为 2 个像素的采样区域(两行四列),第一行需要采样 4 个亮度分量 Y,1 个色度分量组 UV,第二行需要采样 4 个亮度分量 Y,1 个色度分量组 UV。
也即水平方向上,Y分量为全采样, UV 分量组相对于 Y分量做1/4 降采样。
本期思考题
参考推文中的举例,假设原图的 Width x Height = 6 x 8,存储时将 Stride 对齐为 8。当使用 Stride = 8,Width = 4,进行读取和渲染,会出现什么问题?
(我们下期揭秘)